2020军队文职考试岗位能力备考：弄懂“抽屉原理”

2020-01-09 18:37:24

来源：

分享

“抽屉原理”又称“鸽笼原理”，这一原理在解决实际问题中有着广泛的应用，也是考试中数量关系比较常见的题型。“抽屉原理”的应用是千变万化的，用它可以解决许多有趣的问题，并且常常能得到一些令人惊异的结果。下面红师教育研究与辅导专家带大家一起应用这一原理解决相关问题。

要想弄明白“抽屉原理”，首先我们先想明白一个问题，比如4只鸽子飞回3个笼子里，至少有几只鸽子要飞进同一个笼子里?为什么?先思考一下，4只鸽子可以飞进同一个笼子里，而我们要找的是飞进同一个笼子的鸽子的最小值，尽可能每个笼子里都有鸽子，而且要都比较平均才能确保有最小值的情况，如果每个笼子里分一个鸽子，则还剩余1个鸽子没有分，这个鸽子再分下去，则可得到至少有2只鸽子要飞进同一个笼子里。

对于“抽屉原理”， 这种类型的问题，它的原理是：把n个物体放入m个抽屉里(n>m)，如果m÷n=k……b,那么总有一个抽屉里至少放入(k+1)个的物体。

例1.把25枚棋子放入下图的三角形内，那么一定有一个小三角形中至少放入( )枚。

A.6 B.7 C.8 D.9

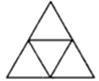
【红师解析】选B。判断题型为“抽屉原理”的应用，25个物品放入4个三角形中，25÷4=6...1，故至少放6+1=7枚

例2.某班有男生25人，女生18人，下面说法正确的是( )。

A.至少有2名男生是在同一个月出生的

B.至少有2名女生是在同一个月出生的

C.全班至少有5个人是在同一个月出生的

D.以上选项都有误

【红师解析】选B。先判断题型为“抽屉原理”的应用，给了男女人数，求同一个月出生的至少几人?月的类型有12个月，即抽屉数为12个。25÷12=2....1,即男生至少有3人在同一月出生，18÷2=1....6，故女生至少有2人在同一个月出生。结合选项，故选B

例3.学校有若干个足球、篮球和排球，体育老师让二(2)班52名同学到体育器材室拿球，每人最多拿2个(可以一个都不拿)，那么至少有( )名同学拿球的情况完全相同。

A.8 B.6 C.4 D.2

【红师解析】选B。题目中总人数为52人，但抽屉数没有告诉我们，先要确定抽屉个数，即总共有多少种情况。不选时，为1种情况;选1个时，有3种情况。选2个时，可选相同类型的，有3种情况，也可选2个不同类型，也有3种情况。故的情况有10种情况，52÷10=5...2，故至少有6个人的拿球情况相同。

以上就是“抽屉原理”的简单应用，理解“抽屉原理”的题型特征，遇到这种类型题目的时能很快判断出来，另外学会解题技巧，做到举一反三。